| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- HTTP
- 웹 서버
- JPA
- 스프링 시큐리티
- 도커
- spring batch
- 스프링 배치
- Container
- CS
- vm
- mysql
- 컨테이너
- 스프링
- 스프링 부트
- 자바
- 데이터베이스
- spring boot
- Spring Security
- 영속성 컨텍스트
- 가상화
- Java
- Spring
- web server
- spring cloud
- 백엔드
- 배포
- CI/CD
- ORM
- virtualization
- computer science
- Today
- Total
개발 일기
[Java] 시간 복잡도 (Time Complexity) - Big-O Notation 본문
알고리즘 문제를 풀어보면 제한 시간이 있는 것을 확인할 수 있다.
시간 복잡도 (Time Complexity)
- 알고리즘에서 시간 복잡도는 주어진 문제를 해결하기 위한 '연산 횟수'로 잡는다. 즉, 소요되는 기본 연산 수에 의거하여 시간복잡도가 계산되는데 여기서 주요 기본 연산으로는 데이터의 비교, 덧셈, 곱셈, 나눗셈 등이 있다.
- 일반적으로 수행 시간은 1억번의 연산을 1초로 잡는다.
- 알고리즘의 성능을 나타내는 지표로, 입력 크기에 대한 연산 횟수의 상한을 의미합니다. 시간 복잡도는 낮으면 낮을 수록 좋다.
- 그런데 이러한 생각이 들었다. '예를들어 1차원 배열의 경우 탐색하고자하는 배열마다 만약 찾고자하는 값이 index 0에 있냐 아님 배열의 가장 마지막 Index에 위치하냐에 따라 연산 횟수가 달라지지 않나?'라는 생각을 했다.


➜ 그렇기 때문에 시간 복잡도는 시작한 순간부터 결과값이 나올때 까지 연산 횟수를 '최선(best case)', '보통normal(average case)', '최악(worst case)' 이렇게 3개로 나눌 수 있다.
시간 복잡도를 계산할때 기본적으로 점근적 표기법을 사용하고 예를들어 입력값 n에 대해서 4n2+3n+4 번 만큼 계산하는 함수가 있다면, 최고차항만 고려하고 계수는 무시하며 최악(worst case)의 상황을 고려하여야 한다.

점근적(Asymptotic) 표기법
알고리즘의 성능은 입력의 크기가 충분히 클 때의 성능이 중요하다. 그래서 알고리즘의 수행 시간은 항상 입력의 크기가 충분히 클 때를 분석한다. 즉, 입력이 ∞일 때를 분석하기 위해 점근적 분석이 필요하다.

빅오 표기법(Big-O Notation) - 점근적 상한선
아무리 나빠도 시간이 이보다 덜 걸림. 즉, 최악의 시나리오
위에서 얘기한 최악의 상황을 고려할 수 있는 표기법이 바로 이 빅 오 표기법이다. 알고리즘이 처리해야 할 데이터의 양이 증가할 때, 알고리즘의 최악의 상황으로 실행 시간이 어떻게 증가하는지를 나타내는 데 초점을 맞춘다. 즉, 입력 크기가 무한히 커질 때 알고리즘의 실행 시간이 어떻게 증가하는지를 설명한다.

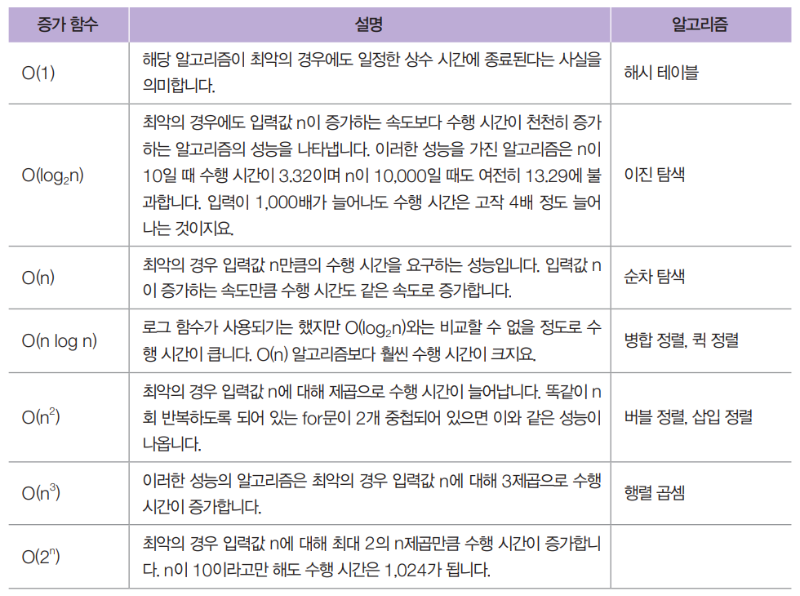
O(1) - Constant Time Complexity
- 설명: 알고리즘의 시간 복잡도가 O(1)인 경우, 입력값(N)의 크기와 상관없이 항상 일정한 시간이 소요됩니다. 즉, 데이터의 크기가 커져도 실행 시간이 변하지 않는 특징이 있습니다. 이는 일반적으로 기본 연산(assignment, arithmetic operation, array indexing 등)이 이에 해당합니다.
- 예시: 스택의 push와 pop 연산은 항상 마지막 요소에 접근하거나 추가/삭제하는 작업으로, 입력값의 크기와 무관하게 일정한 시간 내에 처리됩니다.
O(log N) - Logarithmic Time Complexity
- 설명: O(log N) 알고리즘은 입력값의 크기가 커질수록 연산 시간이 증가하지만, 그 증가율이 매우 느린 형태입니다. 매번 데이터의 크기가 절반으로 줄어드는 방식으로, 반으로 나누는 과정이 반복되는 알고리즘이 이에 해당합니다. 이 때, 로그의 밑은 2인 경우가 많습니다.
- 예시: 이진 탐색(Binary Search)는 정렬된 배열에서 원하는 값을 찾기 위해 데이터를 계속 반씩 나누며 탐색하기 때문에 O(log N) 시간 복잡도를 가집니다. 또한, 이진 트리의 탐색도 유사한 시간 복잡도를 가집니다.
O(N) - Linear Time Complexity
- 설명: O(N) 시간 복잡도는 입력값의 크기(N)가 커지면 커질수록 실행 시간이 비례해서 증가합니다. 데이터를 한 번씩 모두 검사하거나 순회해야 하는 작업에서 주로 나타납니다.
- 예시: 단일 for문을 사용하여 배열의 모든 요소를 순회하는 알고리즘이 대표적입니다. 예를 들어, 배열에서 특정 값을 찾기 위해 처음부터 끝까지 하나씩 확인하는 경우가 이에 해당합니다.
O(N log N) - Linearithmic Time Complexity
- 설명: O(N log N)은 O(N)과 O(log N)이 결합된 형태로, 데이터의 크기 N에 대해 각 요소에 대해 로그 N 시간이 걸리는 작업이 반복되는 경우입니다. 이는 O(N)보다 느리지만 O(N^2)보다는 빠릅니다.
- 예시: 퀵 정렬(Quick Sort), 병합 정렬(Merge Sort), 힙 정렬(Heap Sort) 같은 정렬 알고리즘이 O(N log N) 시간 복잡도를 가집니다. 이들은 재귀적으로 리스트를 나누고 정렬하면서 병합하거나, 힙 자료구조를 사용하여 정렬합니다.
O(N^2) - Quadratic Time Complexity
- 설명: O(N^2) 시간 복잡도는 N의 제곱에 비례해서 시간이 걸리는 알고리즘입니다. 이는 보통 중첩된 반복문에서 나타나며, 입력값이 커질수록 시간 복잡도가 급격히 증가합니다.
- 예시: 이중 for문으로 배열의 모든 쌍을 비교하는 알고리즘이나, 버블 정렬(Bubble Sort), 삽입 정렬(Insertion Sort), 선택 정렬(Selection Sort)이 O(N^2) 시간 복잡도를 가집니다.
O(2^N) - Exponential Time Complexity
- 설명: O(2^N) 시간 복잡도는 입력값 N이 증가할 때마다 실행 시간이 지수적으로 증가합니다. 이 경우, 작은 입력 크기에서도 연산 시간이 매우 빠르게 커지기 때문에 입력값이 크면 실용적이지 않은 알고리즘이 됩니다. 주로 재귀적으로 문제를 푸는 알고리즘에서 나타납니다.
- 예시: 피보나치 수열을 단순 재귀로 계산할 때, 매번 두 개의 하위 문제로 분할하며, 각 하위 문제에 대해 다시 두 개의 하위 문제로 분할하여 해결하는 방식은 O(2^N) 시간 복잡도를 가집니다.
O(N!) - Factorial Time Complexity
- 설명: O(N!) 시간 복잡도는 N이 증가할수록 N 팩토리얼의 속도로 시간이 증가하는 알고리즘입니다. 이는 모든 가능한 경우의 수를 탐색해야 하는 문제에서 나타나며, 가장 비효율적인 시간 복잡도 중 하나입니다. 입력 크기가 작아도 시간이 매우 오래 걸리기 때문에, 실질적으로 매우 제한적인 상황에서만 사용됩니다.
- 예시: 순열 생성(permutation generation)이나 외판원 문제(Traveling Salesman Problem, TSP)의 완전 탐색 방식이 O(N!) 시간 복잡도를 가집니다. 외판원 문제에서 모든 경로를 탐색하려면 도시 수 N에 대해 N!개의 경로를 모두 조사해야 합니다.
그 뒤로 O(∞) : 종료되지 않는 무한 루프도 있긴하다.
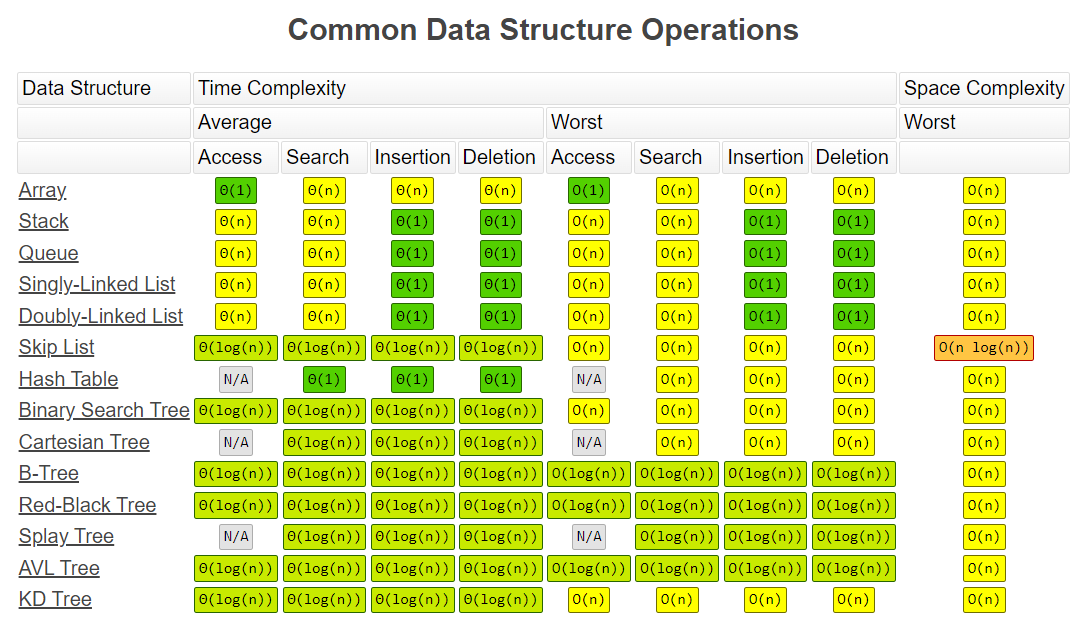
무작정 코드작성하려고 달려들지말고 문제를 읽고 내가 구현하고자하는 알고리즘의 시간 복잡도와 문제에서 주워진 처리해야할 데이터 크기를 1억번의 연산을 1초로 고려하여 계산해보고 비교해보고 가능성 여부를 판단해봐야겠다. 아래는 Data Structure 및 알고리즘 별 시간복잡도다.

'Back-End > Java' 카테고리의 다른 글
| [Java] List 인터페이스 구현체 - ArrayList와 LinkedList (0) | 2024.10.23 |
|---|---|
| [Java] 자료 구조 - Array와 Collection Framework의 인터페이스들 (1) | 2024.10.22 |
| [Java] 자바 기본적인 입출력 방법 비교(Scanner와 BufferedReader 그리고 BufferedWriter) (1) | 2024.10.21 |
| [Java] JDBC(Java DB Connectivity) & HikariCP(Hikari Connection Pool) (0) | 2024.09.21 |
| [Java] 자바 접근 제어자(Access Modifier) 정리 - public/private/protected/default (0) | 2024.06.04 |





